Python program to find the nth Fibonacci Number

If you are interested to learn about the NSEtools in Python

In the following tutorial, we will understand how to find the nth Fibonacci Number using Python. We can define a Fibonacci Number, where the following number is the sum of the preceding two numbers.

The first two elements of the Fibonacci series are 0 and 1, respectively. We can calculate the third element of the series by adding the preceding two elements and will get the third term as 0 + 1, which is equal to 1. Similarly, the fourth term will be the sum of the second and third terms, which is 1 + 1 = 2 and so on. The series of such numbers is known as a Fibonacci Series. The recurrence relation defines a Fibonacci number as shown below:

F_n = F_{n – 1} + F_{n – 2}

There are different ways to find the nth Fibonacci Number using the Python programming language. Some of them are as follows:

1. Finding nth Fibonacci Number using Recursion
2. Finding nth Fibonacci Number using dynamic programming
3. Finding nth Fibonacci Number using dynamic programming and space optimization
4. Finding nth Fibonacci Number using arrays

Of these ways, the two most fundamental are the Recursion method and the Dynamic method.

Let us understand the working of these methods in detail with examples.

What is Fibonacci series in Python?

In this tutorial, we will discuss how the user can print the Fibonacci sequence of numbers in Python. Fibonacci sequence: Fibonacci sequence specifies a series of numbers where the next number is found by adding up the two numbers just before it. 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, … and so on.

What is the formula of Fibonacci?

The Fibonacci formula is given as, F_n = F_n-1 + F_n-2, where n > 1.

Finding nth Fibonacci Number using Recursion

The term recursion is used to define something within itself. In a programming language like Python, Recursion refers to the process of a function calling itself. With the proper and correct code, the Recursion will create a finite loop. Let us consider the following snippet of code for better understanding.

Example:

# defining the function for Fibonacci Series  
def Fibonacci_Series(n):   
    # using if-else conditional statement  
    if n < 0:  
        print("Oops! Incorrect input")  
    # First Fibonacci number is 0  
    elif n == 0:   
        return (0)   
    # Second Fibonacci number is 1   
    elif n == 1:  
        return (1)  
    else:  
        return (Fibonacci_Series(n - 1) + Fibonacci_Series(n - 2))   
# printing the 12th element of the Fibonacci Series  
print("12th Element of the Fibonacci Series:", Fibonacci_Series(12))  

Output:

12th Element of the Fibonacci Series: 144

Explanation:

In the above snippet of code, we have defined a function as Fibonacci_Series() that accepts a parameter as n.

Moreover, we are aware that the first two elements of the Fibonacci are 0 and 1. In the event of the input as n = 1 or n = 2 (First or Second terms of Fibonacci series), we have used the if-else conditional statement to return 0 or 1. In case the value of n is greater than 2, the function will call itself with a lower input value. As we can observe that the code returns (Fibonacci_Series(n – 1) + Fibonacci_Series(n – 2)). Here, the function calls itself with a lower value unless it reaches the base value of n = 1 and n = 2, and as we know from before, n = 1 returns 0 and n = 2 returns 1. The returned values are then continuously added to produce the sequence of the Fibonacci Series.

Finding the nth Fibonacci Number using Dynamic Programming

Dynamic Programming utilizes Recursion as well; however, it mainly utilizes if-else conditional statements. Within the statements, the value of the Fibonacci number is stored in a variable. With the help of Recursion, the repeated addition allows us to obtain this Fibonacci number.

Let us consider the following example to understand the same.

Example:

# defining the function to find the nth Fibonacci Number  
def Fibonacci_series(x):  
    # Taking First two terms of the Fibonacci Series as 0 and 1  
    fib_Array = [0, 1]  
    # Here, as we know that the first two terms of Fibonacci Series are 0 and 1,  
    # we append the remaining values (Fibonacci numbers from index 2 to x)  
    # in the array using recursion and return the last element.   
    # In the range function, we take range(2, x + 1) instead of range(2, x).  
    # This is because range function in python iterates until the value  
    # before the upper limit. So, if we take from 2 to x, it would only  
    # iterate from second to (x - 1)th element.  
    for n in range(2, x + 1):  
        fib_Array.append(fib_Array[n - 1] + fib_Array[n - 2])  
    return fib_Array[x]  
print("12th Term of Fibonacci Series:", Fibonacci_series(12))  

Output:

12th Term of Fibonacci Series: 144

Explanation:

In the above snippet of code, we defined the function as Fibonacci_series(), which accepts the parameter as variable x. We created a one-dimensional array as fib_Array with data elements 0 and 1 in its zeroth and first indices. Then, if the provided input (‘x‘) is less than or equal to 2, which is also the length of the array fib_Array, it returns 0 as the first number for x = 1 and 1 as the second number for x = 2. If the value of x is greater than 2, we have used recursion to call and insert the preceding two data elements. However, rather than returning the nth Fibonacci number directly, we append each of the summated elements to the fib_Array array. At last, we have returned the last element of the array (i.e., the nth element) and printed the value for the users.

Finding the nth Fibonacci Number using Dynamic Programming and Space Optimization

This method is almost completely identical to Dynamic Programming. However, dynamic programming utilizes recursion to accomplish recurring addition, whereas this method utilizes the for-loop. Let us consider the following example to understand the same.

Example:

# defing the function to return the nth element of the Fibonacci Series  
def Fibonacci_series(x):   
    # assiging the variables  
    m = 0  
    n = 1  
    # using the if-elif-else conditional statements  
    if x < 0:  
        print("Wrong input")   
    elif x == 0:  
        return m   
    elif x == 1:   
        return n  
    else:  
        # using the for-loop   
        for i in range(2, x + 1):   
            o = m + n  
            m = n   
            n = o   
        return n   
# printing the twelveth term of the Fibonacci Series  
print("12th element of the Fibonacci Series:", Fibonacci_series(12))  

Output:

12th element of the Fibonacci Series: 144

Explanation:

In the above snippet of code, we have defined a function and assigned two variables, m = 0 and n = 1. These elements are the first and second elements of the Fibonacci Series. We have then used the if-elif-else conditional statements where the program returns 0 for input value x = 1 and 1 for input value x = 2. If the value of x is greater than 2, we have used the for-loop of i in the range (2, x + 1). We have taken a variable o to store the sum of the preceding two elements in the series. Once o takes the value of m + n, the value of m is reassigned to n. Subsequently, the value of n is reassigned to the value of o. This process continues, and value 3 keeps reassigning until the loop terminates. Once the loop is terminated, the function returns the value of n, which stores the value of the nth Fibonacci Number.

Finding the nth Fibonacci Number using Array

In this method, we create an array of size x by repeated addition using the for-loop. Hence, the nth Fibonacci Number is returned.

Let us consider the following example to understand the same.

Example:

# defining the function  
def Fibonacci_series(x):   
  # creating an array in the function  
   fib_Array = [0] * (x + 1)  
   fib_Array[1] = 1  
   # adding elements of the series to the array using addition of previous two elements.  
   for n in range (2, x + 1):  
      fib_Array[n] = fib_Array[n - 1] + fib_Array[n - 2]   
   return fib_Array[x]  
if __name__ == "__main__":  
   print("12th element of the Fibonacci series:", Fibonacci_series(12))  

Output:

12th element of the Fibonacci series: 144

Explanation:

In the above snippet of code, we have defined the function. Within the function, we have created an array to find the nth element of the Fibonacci Series. We have then used the for-loop to add elements of the series to the array by repeating the addition of the preceding two elements. At last, the nth element is returned and printed for the users.

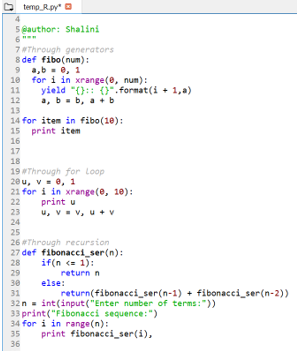
Recursion Method

Example

#recursive approach
def Fibonacci(n):
   if n<0:
      print("Fibbonacci can't be computed")
   # First Fibonacci number
   elif n==1:
      return 0
   # Second Fibonacci number
   elif n==2:
      return 1
   else:
      return Fibonacci(n-1)+Fibonacci(n-2)
# main
n=10
print(Fibonacci(n))

Output

34

The scope of all the variables declared is shown below.

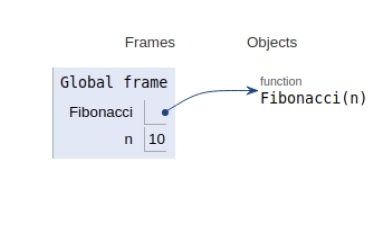
Programming Method

Example

#dynamic approach
Fib_Array = [0,1]
def fibonacci(n):
   if n<0:
      print("Fibbonacci can't be computed")
   elif n<=len(Fib_Array):
      return Fib_Array[n-1]
   else:
      temp = fibonacci(n-1)+fibonacci(n-2)
      Fib_Array.append(temp)
      return temp
# Driver Program
n=10
print(fibonacci(n))

Output

34

The scope of all the variables declared is shown below

Methods Through which Fibonacci Series can be Generated

Below are the three methods through which the Fibonacci series can be generated:

1. Through Generators

Code:

def fibo(num):
  a,b = 0, 1
  for i in xrange(0, num):
    yield "{}:: {}".format(i + 1,a)
    a, b = b, a + b
for item in fibo(10):
  print item

Output:

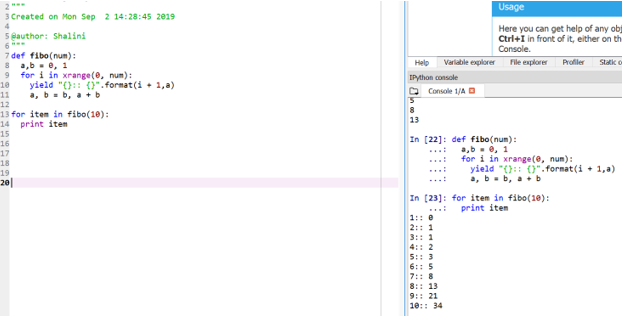
This method is referred to as “generator” because the function xrange is a generator of the numbers between 0 and num, and yield is the generator for formatted output.

Here is What xrange does for you:

Here Fibonacci series has been defined in the form of function, inside which for loop, xrange and yield function takes care of the output.

2. Through for loop

Code:

u, v = 0, 1
for i in xrange(0, 10):
    print u
    u, v = v, u + v

Output:

As one can see, a simple for loop has been used to print the Fibonacci series between 0 to 10. Inside for loop, new values have been assigned to the variables. U and v are the default initial values of Fibonacci that have been set to 0 and 1, respectively. As for the loop progresses to run, the new u value is the old v value, whereas the new v value is the sum of old values of u and v. This continues till the end of range values.

3. Through Recursion

Code:

#Through recursion
def fibonacci_ser(m):
    if(m <= 1):
        return m
    else:
        return(fibonacci_ser(m-1) + fibonacci_ser(m-2))
m = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(m):
    print fibonacci_ser(i),

Output:

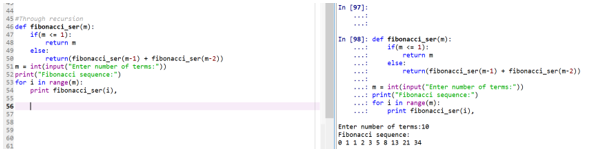
• The function “fibonacci_ser” is making the call to itself to print the Fibonacci series.
• And hence the method has got its name “recursion”.

Steps Followed here:

1. Here the user has been asked to input the place till which the Fibonacci series needs to be printed.
2. Number passes through the function “fibonacci_ser”.
3. The condition gets checked if the length provided is less than 1 or not. If yes, the result is given immediately.
4. However, if the length is greater than 1, recursive calls are made to “fibonacci_ser” with arguments having length lesser than 1 and 2, i.e. fibonacci_ser(m-1) and fibonacci_ser(m-2).
5. Hence, recursion gives the desired output and print it.

• So, in short, We discussed Three ways for displaying the Fibonacci series.
• Through for loop, through generators and through recursion.

All Three Python Code’s Summarized

Below are the three python code:

1. Through Generators

Code:

def fibo(num):
  a,b = 0, 1
  for i in xrange(0, num):
    yield "{}:: {}".format(i + 1,a)
    a, b = b, a + b
for item in fibo(10):
  print item

2. Through for loop

Code:

u, v = 0, 1
for i in xrange(0, 10):
    print u
    u, v = v, u + v

3. Through Recursion

Code:

def fibonacci_ser(n):
    if(n <= 1):
        return n
    else:
        return(fibonacci_ser(n-1) + fibonacci_ser(n-2))
n = int(input("Enter number of terms:"))
print("Fibonacci sequence:")
for i in range(n):
    print fibonacci_ser(i),

Summarized above are all procedures; one needs to practice to get a good grip on all.

Output: